Learning how Edward Kmett’s bound library worked was quite a challenge for me. Even though there is a nice tutorial, I found it rather difficult to penetrate – the puns, while humorous, didn’t help either. Moreover, polymorphic recursion itself is a rather strange concept that takes some getting used to.

In the end, I had to read through code very carefully in order to understand the inner workings of the library. In the process, I made some sketches to guide myself. Not surprisingly, the pictures themselves explain the concept much more clearly than the code or the text! (At least I found that to be the case, YMMV.)

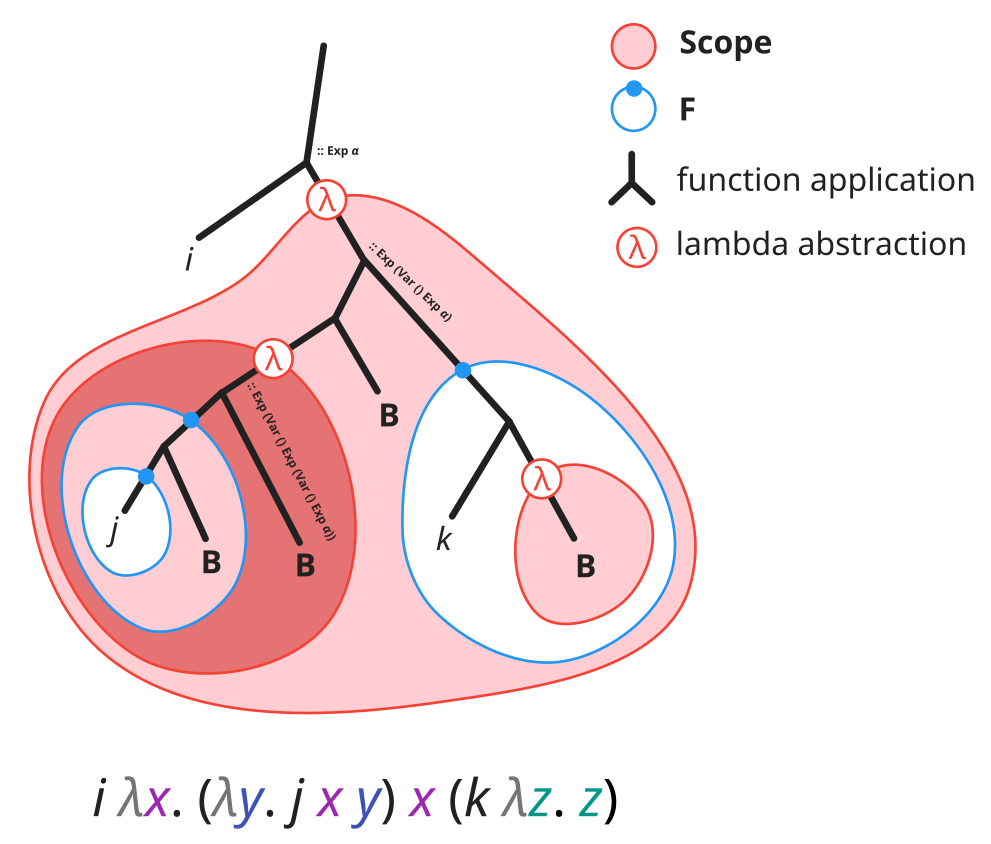
Here’s a picture that shows an expression tree in untyped lambda calculus. Click to zoom in! (You can also get the SVG version.)

There are a couple interesting things to note:

• Important observation: for a given expression there are multiple distinct representations! This is how the library manages to be efficient (what Edward refers to as “you can lift whole trees”). However, this is for all intents and purposes an implementation detail: whenever you test for equality using (==), the representation is automatically canonicalized. Note that the tree show above is not canonical.

• The F node negates the effect of the enclosing Scope on its children . Nested F nodes will negate additional nested Scopes, until there are no more Scopes to negate. This is enforced by the type system, so you can’t screw this up by accident.

  F nodes can be pushed towards the leaves: in doing so, it replicates itself whenever it encounters a fork in the tree. Pushing every F node to the leaves produces the canonical representation.

• The B leaf binds to the prevailing Scope − i.e. the innermost scope that isn’t negated. If all Scopes have been negated, then B leaves cannot appear (also enforced by the type system).

  If the type variable b is not (), then one needs to also specify the which subvariable of the prevailing Scope it should bind to. This is used to bind multiple variables simultaneously.

• Monadic bind (>>=) applies the given function to every variable and grafts the result in its place. This is used in substitution, a.k.a. instantiation.

• Lifting creates a Scope from an existing expression. In traditional implementations based on de Bruijn indices, this would require a traversal of the entire expression, but in the bound library this is done simply by wrapping the entire tree inside F, which negates the effect of the enclosing Scope.

  Lifting occurs whenever an expression needs to be substituted into something that is deeper in scope.